2133. Принадлежность точки лучу
Определите, принадлежит ли заданная точка лучу.
Вход. Шесть целых чисел
– координаты точки и координаты начала и конца вектора. Все числа не превышают
по модулю 10000.
Выход. Одна строка – “YES”, если точка
принадлежит лучу, и “NO” в противном случае.
|
Пример
входа |
Пример
выхода |
|
1 6 3 7 5 8 |
NO |
РЕШЕНИЕ
геометрия
Анализ алгоритма
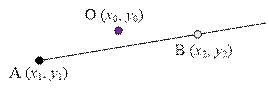
Пусть O(x0,
y0) – координаты точки, A(x1, y1) – координаты вершины луча, B(x2, y2)
– координаты точки, лежащей на луче.
Сначала следует проверить, лежит ли точка O на прямой AB. Для
этого вектора AB (x2 – x1, y2 – y1) и AO (x0 – x1, y0 – y1) должны быть колинеарными:

или то же самое
что
(x0 – x1) * (y2 – y1)
= (x2 – x1) * (y0 – y1)
Точки O и B
должны находиться по одну сторону от вершины луча A.

Это условие
следует записать как для координаты x,
так и для y:
 и
и 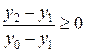
или для избежания деления то же самое
что
(x0 – x1) * (x2 – x1)
≥ 0 и (y0 – y1) * (y2 – y1)
≥ 0
Реализация алгоритма
Реализуем
проверку принадлежности точки лучу согласно выше приведенным условиям.
scanf("%d %d %d %d %d %d",&x0,&y0,&x1,&y1,&x2,&y2);
if (((x0 - x1) * (y2 - y1) == (x2 - x1)
* (y0 - y1)) &&
((x0 - x1) * (x2 - x1) >= 0) && ((y0 - y1) * (y2 - y1) >= 0))
printf("YES\n");
else printf("NO\n");